Aprendizaje conceptual
Find-S
¿Qué pasa si queremos que las hipótesis sean disynciones (or) en vez de conjunciones (and)?
Ejemplo: Dedicación == 'Alta' OR Horario == 'Nocturno'
La formula sería: <'Alta',
El algoritmo comenzaría con:
<
Pero el siguiente paso tendría más de una opción de hipótesis más general que además confirmen el primer ejemplo de la tabla (
Ej: <Alta,
A su vez, ya no podemos ignorar los ejemplos negativos.
Candidate elimination
Sesgos
Sesgo Inductivo: del algoritmo L es el conjunto mínimo de suposiciones B tales que:
Para que un algoritmo aprenda, debe tener algún sesgo inductivo.
Sesgo preferencial: el algoritmo prefiere ciertas hipótesis sobre otras.
Ej.: ID3 o Find-S
Sesgo restrictivo: se maneja un espacio de hipótesis incompleto.
Ej.: Naive Bayes
Arboles de decisión
...
Metodología para clasificación
Tratamiento de atributos numéricos o categóricos
Numéricos:
KNN -> re-escalado o normalización
Aprendizaje conceptual, ID3 y Naive Bayes -> particionar en intervalos.
ID3 puede hacerlo en el paso recursivo de manera que maximice la ganancia de elegir ese atributo.
Categóricos:
KNN, Redes Neuronales, Regresión Lineal y Logística:
label-encoding si hay orden total en los valores, one-hot-encoding si no.
Medidas de performance
Accuracy: ¿cuántos casos predice h correctamente?
Combinando precisión y recuperación se obtiene la medida-F:
Ejemplo
| A | h(x)=a | h(x)=b | h(x)=c | Total |
|---|---|---|---|---|
| y=a | 30 | |||
| y=b | 30 | |||
| y=c | 40 | |||
| 23 | 41 | 46 | 100 |
micro y macro average
- Se calcula la medida por clase, y luego se promedia los valores obtenidos (macro average).
- Se calcula la medida por clase teniendo en cuenta el aporte de instancias cada clase (micro average).
En el ejemplo anterior:
- La macro-average de la precision será
- La micro-average será
¿Qué medida es más "útil"?. Como toda medida, depende de lo que queremos evaluar:
- La micro-average da más peso a las clases grandes en el análisis general
- La macro-average permite evaluar mejor que tan "equilibrado" es el comportamiento de mi clasificador
- En lo posible, reportar ambas y analizar según mi problema
Evaluación de hipótesis
Si:
- Nuestras hipótesis toman valores discretos
- Nuestras instancias son independientes entre sí, y de la hipótesis
Entonces:
- Un estimador no sesgado de
- El 95% de las veces,
Aprendizaje Bayesiano
probabilidad condicional
- Refleja el nivel de confianza de
- Refleja el nivel de confianza de
hipótesis MAP
La ‘mejor’ hipótesis es la hipótesis más probable dados los datos, que maximiza
Dado que los datos de entrenamiento siempre son los mismos, P(D) no cambia, por lo tanto:
hipótesis ML (máxima verosimilitud)
Bajo la hipótesis que
naive bayes
Asume independencia de los atributos dada una hipótesis.
O sea:
m-estimador
Donde:
-
- Cantidad de veces que el atributo vale lo querés dada la hipótesis
- ej: Cantidad de ejemplos donde el tiempo es nublado y el niño no jugó
-
- Es decir, la cantidad de veces que se dio la hipótesis
- ej: Cantidad de veces que el niño jugó
-
- Es la cantidad de ejemplos que querés añadir.
-
- Es la probabilidad de que se dé el valor del atributo que querés.
- ej: tiempo nublado
- Se puede tomar equiprobable:
Aprendizaje basado en casos
La idea es crear un clasificador ‘perezoso’ para clasificar una nueva instancia, utilizo aquellas que más se le parecen de las que ya conozco.
Ventajas:
- Para cada nueva instancia puedo obtener un clasificador diferente.
- La descripción de las instancia puede ser tan compleja como quiera.
Desventajas:
- El costo de clasificación puede ser alto.
- Atributos irrelevantes pueden afectar la medida de similitud.
K - Nearest Neighbor
Queremos aproximar un concepto, utilizando las k instancias más
cercanas a un elemento <a1,...,an> que deseamos clasificar.
- Se pueden usar muchas nociones de distancia.
- Si los diferentes atributos tienen distinta magnitud: escalar o normalizar.
- Si hay atributos más relevantes que otros: ponderar al calcular la distancia.
- Si hay atributos categóricos sin definición de distancia natural: one-hot-encoding.
Elección de K
- Si se elige k muy bajo, el resultado es muy sensible al ruido; si es muy alto, las zonas que tengan muchos ejemplos pueden acaparar a zonas que tengan menos.
- Por lo general se elige un k impar para no tener problemas de empate.
- Una forma de estimar k es probando distintos valores, midiendo la performance dejando un elemento del conjunto afuera y clasificando con el resto (1-out-cross-validation).
¿Cuál es el sesgo inductivo de K-NN?
La clasificación de una instancia es parecida a las de sus k vecinos (cercanía implica similitud).
Regresión local ponderada
Generalizamos KNN, creando una aproximación local de la función objetivo y construimos una función h que aproxime a los puntos cercanos a
- Varias elecciones para la función
- Media sobre los k vecinos cercanos
- Ponderado a todo el conjunto de instancias
- Ponderado a los k cercanos
Luego de clasificar la nueva instancia, podemos descartar a la hipótesis encontrada: cada instancia genera una nueva aproximación.
Razonamiento basado en casos
Al igual que KNN y RLP, clasificamos una instancia en base a casos parecidos: en lugar de puntos en un espacio euclídeo, las instancias se representan con atributos más complejos.
- Se debe buscar una métrica de similitud que depende del dominio de trabajo.
- La solución se basa en combinaciones complejas y específicas al dominio de aplicación.
Aprendizaje No Supervisado
En el aprendizaje no supervisado trabajamos directamente con las instancias sin anotar, buscando patrones y relaciones dentro del conjunto.
Clustering
- Buscamos agrupar las instancias del conjunto de entrenamiento
- Queremos que las instancias que están en el mismo cluster sean parecidas entre sí, y diferentes a los de los demás clusters.
- Podemos también verlo como un proceso de clasificar... con etiquetas desconocidas.
- El objetivo del clustering no es predictivo, sino descriptivo.

Para determinar qué tan parecidas son las instancias, se usan las distancias.
- distancia euclídea
- distancia coseno
- etc...
K-means
- Asume que nuestras instancias pertenecen a
- Es un algoritmo de partición: parte el espacio en K clusters convexos.
- Cada cluster está representado por un centroide (definido como la media de las instancias).
- Se busca minimizar la distancia euclídea entre los puntos de cada cluster y su centroide.

- El centroide de un cluster se define como la media de las instancias (
- Lo que querríamos tener es un conjunto de clusters donde fuera mínima la suma de los errores cuadráticos (SSE):
- Problema: probar todas las combinaciones posibles de clusters es muy costoso.
- K-means propone una aproximación iterativa, que tiene complejidad lineal en el número de instancias.
Input: S (dataset), K (número de clusters)
Output: clusters
1: Inicializar K centroides aleatoriamente
2: Mientras no se de la condición de fin:
3: Asignar cada instancia al centroide más cercano
4: Recalcular los centroides
5: Retornar los clusters
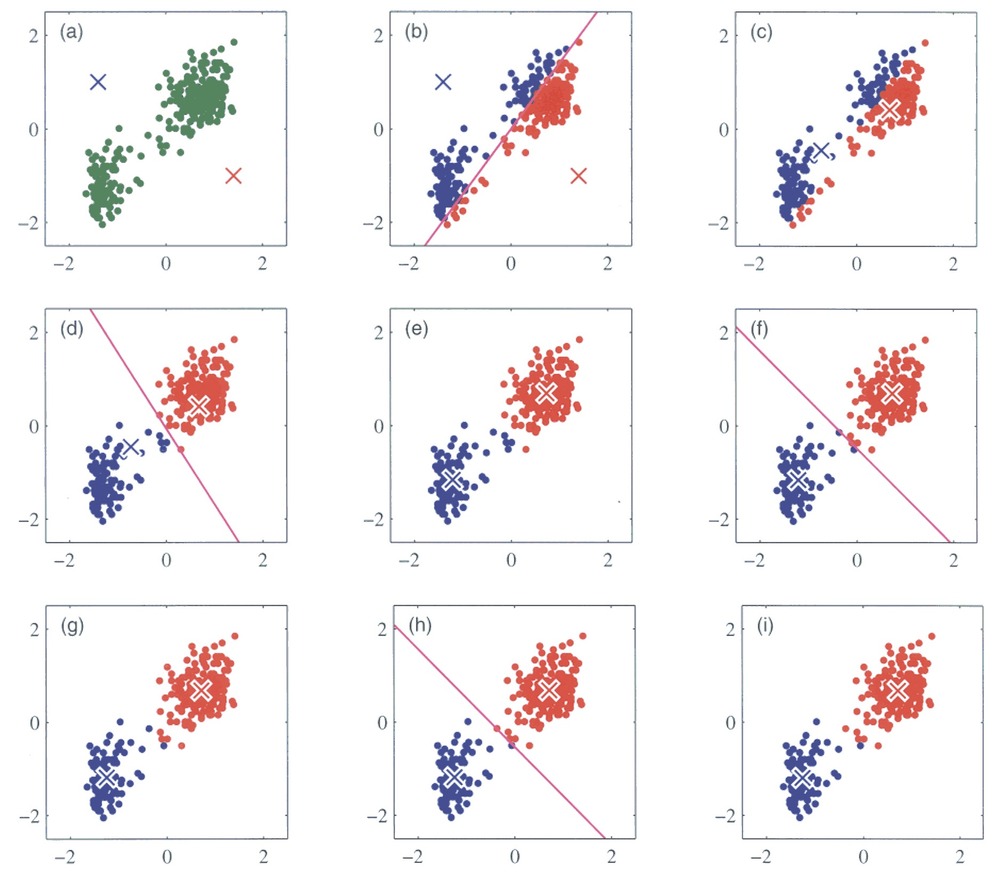
- K-means es bueno cuando los clusters son isotrópicos (uniformes en todas direcciones).
- Problema: muy sensible a la inicialización.
- Heurística:
- probar diferentes inicializaciones y elegir aquella donde
- elegir como centroides iniciales puntos del dataset.
- probar diferentes inicializaciones y elegir aquella donde
Evaluación externa
Necesitamos una forma de comparar el clustering generado con el derivado de las clases.
La medida más utilizada es el índice de Rand:
- Dados dos agrupamientos
-
-
-
-
- El
- El RI resulta en un valor entre 0 y 1, donde 0 indica que los clusters no concuerdan en ningún par, y 1 indica que los clusters son exactamente iguales
- El problema con RI es que si asignamos clusters al azar, no necesariamente nos da 0. El Adjusted Rand Index es una versión donde se busca corregir la influencia del azar, ajustando a partir de una matriz de contingencia.
Evaluación interna
No tenemos clusters "verdaderos", tenemos que hacer una validación interna.
La validación interna busca medir principalmente la cohesión de los clusters, y su separación.
El Índice Davies Boulding: mide la similitud promedio entre cada cluster y el cluster más similar a él. Si construimos una matriz que balancea la distancia promedio
Número de clusters
-
No es fácil identificar un número "óptimo" clusters.
-
En general, si aumentamos el número de clusters, nuestros clusters son "mejores".
-
... pero corremos el riesgo de sobre-ajuste.
-
Método del Codo: buscar el punto donde agregar más clusters no vale la pena porque la mejora deja de ser importante.
- dibujar la performance (medida, por ejemplo en SSE) como función de la cantidad de clusters;
- seleccionar el valor correspondiente al codo de la curva.
Principal Component Analysis
- PCA es un método no supervisado para encontrar patrones en los datos.
- Buscar reducir las dimensiones del conjunto de datos, con la mínima pérdida de información posible.
- Muy útil para visualizar datos en espacios n-dimensionales.
Aprendizaje por refuerzos
Está bastante resumido en:
Aprendizaje Por Refuerzos
Regla de actualización, luego de dar un paso del estado
Regresión Lineal
Definición
La regresión lineal es una forma de aprendizaje supervisado donde, a partir de un vector

Función de costo
La función de costo es aquella que mide qué tan cercano es
MSE
Ecuaciones normales y desventajas
Las ecuaciones normales proveen una forma cerrada de calcular los valores de
Descenso por gradiente
Es un algoritmo de búsqueda iterativo, que parte de una estimación inicial de
El algoritmo comienza con un
Regresión Logística
Se aplica la función logística a la salida de la regresión lineal, y sobre eso se establece una barrera de decisión.
Función logística:
Redes neuronales
Matriz de pesos
En general:
La matriz
Bias o sesgo
De manera similar